Система древнерусских саженей: Происхождение саженей из числового ряда Фибоначчи.
Современные учебники истории говорят о том, что Русь «образовалась» тысячу лет назад при крещении, когда «варвары, говорящие непонятно на каком языке...»обрели истинную веру и знания. По этой же версии всё, чего мы достигли привнесено из более древних цивилизаций:
египетской, греческой и европейской. Нас убеждают, что и строить нас, опять-таки, научили греки, итальянцы и прочие иноземцы. Однако огромное количество фактов и проведённый анализ показал, что в древнерусском «Всемере» были заложены знания, использовавшиеся не только русскими зодчими, но и зодчими других народов. Эти знания несли в себе глубокую информацию о гармонии мироздании, отражённую в числах.
Различные авторы по-разному определяют время возникновения саженей. По мнению одних, большая часть саженей у славян образовалась в XII—XIII веках и развивалась примерно до XVII века. Некоторые считают, что она собрана с миру по нитке, «занесена на русскую равнину, вероятно, задолго до утверждения там славян, в III—II веках до Рождества Христова, из Пергама через малоазиатские греческие колонии». Кто-то полагает, что сажень привнесена в Древнюю Русь из других сопредельных или отдаленных стран.
Утверждается, что церковная сажень имеет в основе древнеримские пассы, греческая — греческие оргии, великая сажень — шведский межевой локоть, а царская — египетский царский локоть… Иными словами, славянский народ был не способен ввести единый измерительный инструмент и потому бессознательно собирал и диспропорционально использовал знания, наработанные соседними народами. С этих позиций даже предположение о возможности существования строгой пропорциональной системы древнерусских саженей представляется просто невероятным.
Однако архитектору А.А. Пилецкому удалось получить схему, отображающую системную зависимость между саженями Древней Руси. Используя ее, он пришел к построению системы пропорций, которую условно назвал «Древнерусским Всемером». Получилась своего рода числовая матрица. И ее важнейшая особенность заключается в том, что она впервые показала глубинную суть древнерусских саженей, которые, как оказалось, имеют золотую пропорцию!
Больше того, «Древнерусский Всемер» превращает отдельные — вроде бы не связанные между собой — измерительные инструменты определенной длины в систему соразмерных, пропорциональных «золоту» длин, образующих поле взаимосвязанных чисел — матрицу. Она и обусловливает числам органическую взаимосвязь всех саженей. Есть и другие особенности.
«Древнерусский Всемер» А.Пилецкого — важнейшее историческое, культурное и архитектурное открытие XX века в России. Мы восстановили необыкновенный инструмент. Он определяет весь процесс зодческого творчества древности. Этот инструмент позволяет получать принципиально новые (точнее — полностью утраченные) числовые взаимосвязи, отображающие пропорциональное «золоту» совмещение длин саженей.
Остается лишь понять случайные ли числа попали в систему мер или же происхождение их чем то обосновано.
Можно предположить, что числовой основой этой системы является натуральный ряд Фибоначчи. На базе натурального числового ряда, используя метод А.А.Пилецкого - А.Ф.Черняева «удвоения и раздвоения чисел», получаем таблицу натуральных чисел.
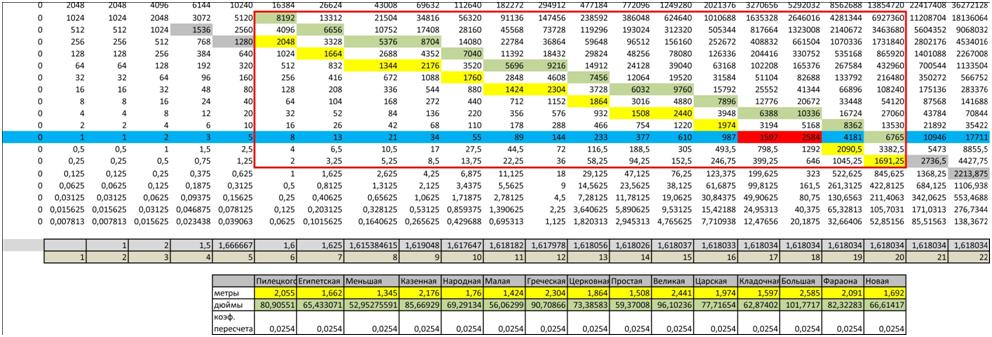Схема 1. Таблица натуральных чисел ряда Фибоначчи с удвоением (вверх от ряда) и раздвоением (вниз от ряда) с выложенными группами саженей (желтый ряд) в метрической системе мер и английской дюймы (зеленый ряд).
Внизу таблицы выложена система саженей по версии Черняева А.Ф. с наименованиями саженей. Натуральный ряд чисел Фибоначчи выделен голубым цветом. В этом ряду 17 и 18 число совпадают численно с Кладочной (1,597 м) и Большой (2,585 м) саженями. При рассмотрении полной таблицы находим полный ряд саженей, вычисленный по методу А.Ф.Черняева в метрической системе мер. За основу взяты длины саженей XII-XVIвв.
Предполагая возражения об отсутствии метрической системы мер в Древней Руси, проведем наложение саженей в английской системе мер.
Рассмотрим теперь английскую систему.
Английская мера длины, заимствована при Петре I для упрощения кораблестроительных заказов за рубежом. При этом для точного соответствия 7 английским футам была немного уменьшена длина сажени. 1 дюйм=0,0254м.
Как видно из таблицы совпадение рядов чисел саженей как в метрической, так и в английской системах мер и табличных значений довольно точное, из чего можно сделать вывод, что:
1.Натуральный ряд чисел Фибоначчи является основой системы саженей Древней Руси.
Кроме того анализ чисел показывает, что числа сажени в 6-м столбце и 19 отличаются незначительно (2048 и 2090), то же самое происходит и с следующей парой чисел – столбец 7 и 20 (1664 и 1691). Таким образом ЦИКЛ составляет 13 чисел из чего заключаем:
2.Базовое количество саженей - 13 штук.
И еще: поскольку числа столбцов 6-10 еще не «набрали зрелость», т.е. соответствуют числу ϕочень грубо, то наиболее точными величинами саженей можно принять значения вычисленные по «Русской матрице» А.Ф. Черняева.
Почему же метрическая система так точно совпала с численным рядом?
Соотношения золотой пропорции исследователи находят в морфологической структуре растений, птиц, животных, человека. Закономерности золотой пропорции обнаруживаются и в организации неорганической природы. Наша Земля часть системы живущей по закону числа ϕ . А теперь остается вспомнить откуда у нас эта самая «метрическая система»: «…Метрическая система выросла из постановлений, принятых Национальным собранием Франции в 1791 и 1795 годах по определению метра как одной десятимиллионной доли одной четверти земного меридиана от Северного полюса до экватора (Парижский меридиан)…»
Вероятно это еще одно подтверждение всеобщей гармонии Мира.
…И умения инженеров XVIII века правильно мерить меридианы.
Вернемся теперь к самому ряду чисел. Число наиболее точным образом можно получить через формулу золотой пропорции ϕ=(1+√5)/2=1,618033989. В числовом ряду Фибоначчи это отношение возникает между 26 и 25 числами и далее его значение неизменно в 9 знаках после запятой. Следовательно, взяв за основу 26 число можно построить числовой ряд в обратную сторону, через известное нам теперь точное отношение чисел. Ряд приобретает свойство бесконечности в убывающую сторону, место нуля занимает число 0,447213595.
Построив по полученному числовому ряду таблицу «удвоений» получаем следующий вид:
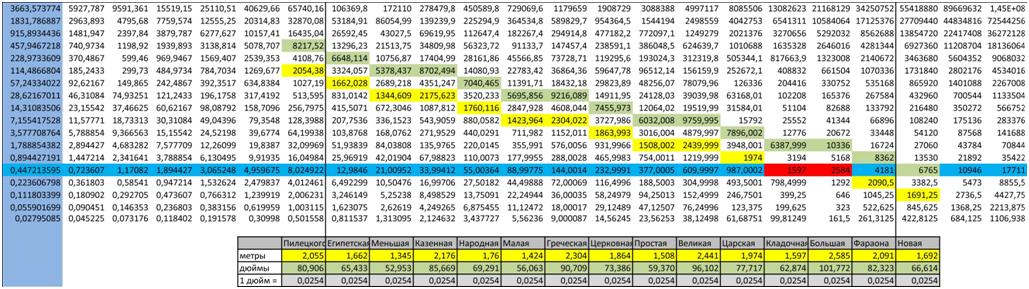
Совпадение саженей практически абсолютное. Причем число 2584 целое и не дает дробных величин в 3х порядках раздвоения. По видимому именно этот столбец число является «осью» системы нашего мироустройства, минимальное целое число в этом столбце = 323. Вероятно, именно этот ряд чисел может быть принят за горизонтальную ось.
Что касается дюймов – возможно система пересчета «метры/дюймы» будет корректнее, если считать дюйм = 0,025м, а не 0,0254.
И еще раз о числовом ряде Фибоначчи. Из 3 схемы видно, числовой ряд бесконечен и безначален и состоит только из положительных чисел.
Зглянем в энцикопедию:
«Древний Египет ,Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные. Исключение составлял Диофант, который вIII веке уже знал правило знаков и умел умножать отрицательные числа. Однако он рассматривал их лишь как промежуточный этап, полезный для вычисления окончательного, положительного результата.
Впервые отрицательные числа были частично узаконены в Китае , а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или, как у Диофанта, признавались как временные значения. Умножение и деление для отрицательных чисел тогда ещё не были определены. Полезность и законность отрицательных чисел утверждались постепенно. Индийский математик Брахмагупта ( VII век ) уже рассматривал их наравне с положительными.
В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Первое описание их в европейской литературе появилось в "Книге абака" Леонарда Пизанского (1202 год), который трактовал отрицательные числа как долг. Бомбеллии Жирар в своих трудах считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения нехватки чего-либо. Даже в XVII веке Паскаль считал, что, так как ничто не может быть меньше, чем ничто. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия».
Подводим итог:
Числовая система Древней Руси была основана на бесконечном и безначальном ряде чисел Фибоначчи.
При удвоении и раздвоении исходного числового ряда, поученные числа проявляют свойства цикличности. Цикл состоит из 13 чисел.
Числа ряда Фибоначчи являются только положительными.
© М.Ю.Макарова 15.10.2012г.
Автор разрешает использование материалов,
опубликованных в данной статье, при условии ссылки на данную статью